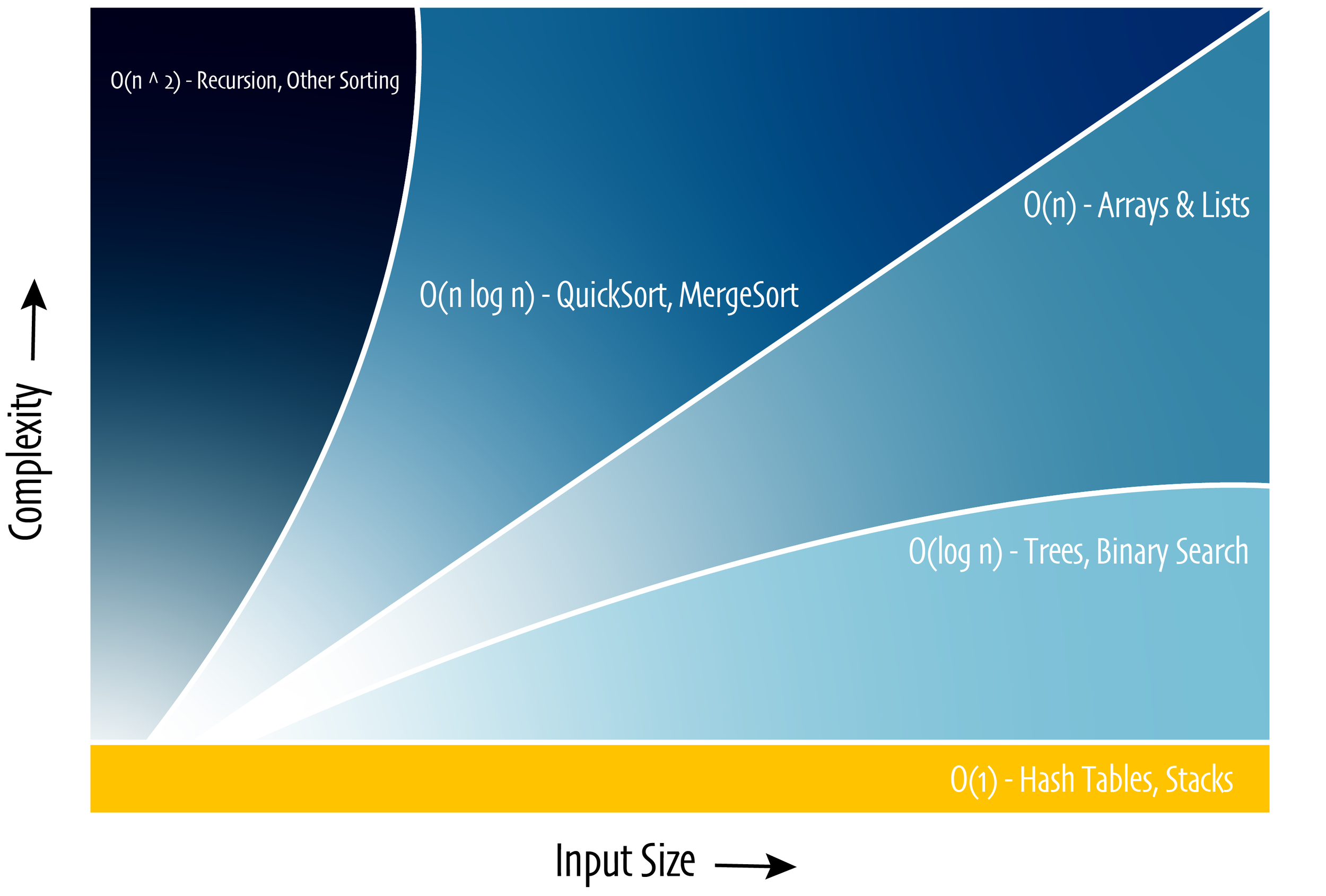
When preparing for technical interviews, it’s vital to develop the skill to prove the effectiveness of your code. Known as asymptotics, the notion of tracking algorithmic performance reveals much about a solution's effectiveness. Ironically, this area of study was primarily developed before the introduction of modern computing. Today, this provides an advantage when testing new ideas and communicating with other developers. In computer science, asymptotics is expressed in a standard format known as Big-O Notation.
Common Runtimes
While there are many standard Big-O run times, the ones illustrated should provide you with a great foundation for the many computer science questions you’ll encounter.
O(n) - Linear Time
The performance of the algorithm is directly related to the size of the input. Examples includes standard functionality found in Arrays and basic Linked Lists.
O(log n) - Logarithmic TIme
The algorithm performs on a logarithmic curve based on the size of the input. Examples includes the binary search and heapsort algorithms as well as Binary Search Trees (data structure).
O(1) - Constant Time
The performance of the algorithm does not vary depending on the size of the input. Examples include operations associated with Hash Table and Stack data structures.
O(n ^ 2) - Exponential Time
The performance of the algorithm decreases exponentially depending on the size of the input. Ironically, many pure sorting algorithms fall into this category including the insertion, selection and bubble sort. If not coded correctly, some recursive algorithms can also perform at O( n ^ 2) time.
How to Study
While there are many topics, you should measure your progress by a). recognizing each algorithm / data structure and b). knowing you could converse with a hiring manager or fellow developers on said topic. Start by checking off items you know and work your way through the topics as you master each item.
Be sure to check out my book for more practical code-based examples in Swift. Once you think you've got things covered, review my top 20 computer science questions then register for my next free class.
Common Data Structures
Data Structures act as the container for holding our data. This is analogous to a pitcher / vessel holding water (e.g. data). Our data can take many forms and complete certain functions depending on the container that holds the information.
| Time Complexity | ||||||
|---|---|---|---|---|---|---|
| Average | Worst Case | |||||
| Search | Insert | Delete | Search | Insert | Delete | |
| Singly Linked List | O(n) | O(n) | O(n) | O(n) | O(n) | O(n) |
| Doubly Linked List | O(n) | O(n) | O(n) | O(n) | O(n) | O(n) |
| Stack | O(1) | O(1) | O(1) | O(1) | O(1) | O(1) |
| Queue | O(n) | O(1) | O(1) | O(n) | O(n) | O(1) |
| Binary Search Tree | O (log n) | O (log n) | O (log n) | O (log n) | O (log n) | O (log n) |
| Hash Table | O(1) | O(1) | O(1) | O(1) | O(1) | O(1) |
Sorting Algorithms
The goal of an algorithm is to come up with some predefined recipe to help us solve complex problems more easily. Examples of complex commercial solutions include PageRank for Google, connecting with friends on Facebook or being able to find driving directions through Google Maps. While these sorting algorithms provide a basic overview, other important concepts one should study include traversal techniques such as depth-first and breadth-first search as well as backtracking algorithms.
| Time Complexity | |||
|---|---|---|---|
| Best | Average | Worst | |
| Insertion Sort | O (n ^2) | O (n ^2) | O (n ^2) |
| Selection Sort | O (n ^2) | O (n ^2) | O (n ^2) |
| Bubble Sort | O (n ^2) | O (n ^2) | O (n ^2) |
| QuickSort | O (n log n) | O (n log n) | O (n ^2) |
| MergeSort | O (n) | O (n log n) | O (n log n) |
| HeapSort | O (n log n) | O (n log n) | O (n log n) |
| Binary Search | O (log n) | O (log n) | O (log n) |
Other Study Lists
Thanks for reviewing my Big-O Notation cheat sheet! If you haven’t already, be sure to also review my other lists as they relate to computer science and Swift / iOS development.